In de laatste les hebben we geleerd hoe je decimalen optelt en aftrekt (zie les “Decimalen optellen en aftrekken”). Tegelijkertijd hebben we beoordeeld hoeveel berekeningen vereenvoudigd zijn in vergelijking met gewone breuken van twee verdiepingen.

Helaas met vermenigvuldigen en delen decimalen een dergelijk effect treedt niet op. In sommige gevallen bemoeilijkt de decimale notatie deze bewerkingen zelfs.

Laten we eerst een nieuwe definitie introduceren. We zullen hem heel vaak zien, en niet alleen in deze les.

Het significante deel van een getal is alles tussen het eerste en het laatste cijfer dat niet nul is, inclusief de uiteinden. Het gaat over als het alleen om cijfers gaat, wordt er geen rekening gehouden met de komma.

De nummers die erin zitten aanzienlijk deel getallen worden significante cijfers genoemd. Ze kunnen worden herhaald en zelfs gelijk zijn aan nul.

Beschouw bijvoorbeeld verschillende decimale breuken en schrijf de overeenkomstige significante delen op:

1. 91,25 → 9125 (significante cijfers: 9; 1; 2; 5);
2. 0,008241 → 8241 (significante cijfers: 8; 2; 4; 1);
3. 15,0075 → 150075 (significante cijfers: 1; 5; 0; 0; 7; 5);
4. 0,0304 → 304 (significante cijfers: 3; 0; 4);
5. 3000 → 3 (er is maar één significant cijfer: 3).

Let op: de nullen binnen het significante deel van het getal gaan nergens heen. Iets soortgelijks zijn we al tegengekomen toen we leerden decimale breuken om te zetten in gewone breuken (zie les “Decimalen”).

Dit punt is zo belangrijk, en er worden hier zo vaak fouten gemaakt, dat ik in de nabije toekomst een test over dit onderwerp zal publiceren. Zeker oefenen! En wij, gewapend met het concept van het significante deel, zullen in feite doorgaan naar het onderwerp van de les.

Decimalen vermenigvuldigen

De vermenigvuldigingsoperatie bestaat uit drie opeenvolgende stappen:

1. Schrijf voor elke breuk het significante deel op. Je krijgt twee gewone gehele getallen - zonder noemers en decimalen;
2. Vermenigvuldig deze getallen op een handige manier. Direct, als de cijfers klein zijn, of in een kolom. We verkrijgen het aanzienlijke deel van de gewenste fractie;
3. Ontdek waar en met hoeveel cijfers de komma in de oorspronkelijke breuken is verschoven om het overeenkomstige significante deel te verkrijgen. Voer omgekeerde verschuivingen uit voor het significante deel dat u in de vorige stap hebt verkregen.

Ik wil u er nogmaals aan herinneren dat er nooit rekening wordt gehouden met nullen aan de zijkanten van het significante deel. Het negeren van deze regel leidt tot fouten.

1. 0,28 12,5;
2. 6,3 · 1,08;
3. 132,5 · 0,0034;
4. 0,0108 1600,5;
5. 5,25 · 10.000.

We werken met de eerste uitdrukking: 0,28 · 12,5.

1. Laten we de significante delen van de getallen uit deze uitdrukking opschrijven: 28 en 125;
2. Hun product: 28 · 125 = 3500;
3. In de eerste factor wordt de komma 2 cijfers naar rechts verschoven (0,28 → 28), en in de tweede wordt deze met nog 1 cijfer verschoven. In totaal heb je een verschuiving naar links nodig met drie cijfers: 3500 → 3.500 = 3,5.

Laten we nu eens kijken naar de uitdrukking 6.3 · 1.08.

1. Laten we de belangrijke delen opschrijven: 63 en 108;
2. Hun product: 63 · 108 = 6804;
3. Opnieuw twee verschuivingen naar rechts: respectievelijk met 2 en 1 cijfer. Totaal - opnieuw 3 cijfers naar rechts, dus de omgekeerde verschuiving zal 3 cijfers naar links zijn: 6804 → 6.804. Deze keer zijn er geen volgnullen.

We hebben de derde uitdrukking bereikt: 132,5 · 0,0034.

1. Belangrijke delen: 1325 en 34;
2. Hun product: 1325 · 34 = 45.050;
3. In de eerste breuk wordt de komma 1 cijfer naar rechts verplaatst, en in de tweede - met maar liefst 4. Totaal: 5 naar rechts. We verschuiven met 5 naar links: 45.050 → .45050 = 0,4505. De nul werd aan het einde verwijderd en aan de voorkant toegevoegd om geen “kale” decimaalteken achter te laten.

De volgende uitdrukking is: 0,0108 · 1600,5.

1. We schrijven de belangrijkste delen: 108 en 16 005;
2. We vermenigvuldigen ze: 108 · 16.005 = 1.728.540;
3. We tellen de cijfers achter de komma: in het eerste getal zijn er 4, in het tweede zijn er 1. Het totaal is weer 5. We hebben: 1.728.540 → 17,28540 = 17,2854. Uiteindelijk werd de “extra” nul verwijderd.

Tenslotte de laatste uitdrukking: 5,25 10.000.

1. Belangrijke delen: 525 en 1;
2. We vermenigvuldigen ze: 525 · 1 = 525;
3. De eerste breuk wordt 2 cijfers naar rechts verschoven, en de tweede breuk wordt 4 cijfers naar links verschoven (10.000 → 1,0000 = 1). Totaal 4 − 2 = 2 cijfers naar links. We voeren een omgekeerde verschuiving uit met 2 cijfers naar rechts: 525, → 52.500 (we moesten nullen toevoegen).

Let op laatste voorbeeld: Omdat de komma in verschillende richtingen beweegt, wordt de totale verschuiving gevonden via het verschil. Dit is erg belangrijk punt! Hier is nog een voorbeeld:

Beschouw de getallen 1,5 en 12.500. We hebben: 1,5 → 15 (schuif 1 naar rechts); 12.500 → 125 (schuif 2 naar links). We "stappen" 1 cijfer naar rechts en vervolgens 2 naar links. Als resultaat zijn we 2 − 1 = 1 cijfer naar links gestapt.

Decimale deling

Verdeling is misschien wel de moeilijkste operatie. Natuurlijk kun je hier naar analogie met vermenigvuldiging handelen: deel de significante delen en "verplaats" vervolgens de komma. Maar in dit geval doen zich veel subtiliteiten voor die de potentiële besparingen teniet doen.

Laten we daarom eens kijken naar een universeel algoritme, dat iets langer is, maar veel betrouwbaarder:

1. Converteer alle decimale breuken naar gewone breuken. Met een beetje oefening duurt deze stap een kwestie van seconden;
2. Verdeel de resulterende breuken op de klassieke manier. Met andere woorden, vermenigvuldig de eerste breuk met de “omgekeerde” tweede (zie les “Numerieke breuken vermenigvuldigen en delen");
3. Presenteer het resultaat indien mogelijk opnieuw als een decimale breuk. Deze stap is ook snel, omdat de noemer vaak al een macht van tien is.

Taak. Zoek de betekenis van de uitdrukking:

1. 3,51: 3,9;
2. 1,47: 2,1;
3. 6,4: 25,6:
4. 0,0425: 2,5;
5. 0,25: 0,002.

Laten we de eerste uitdrukking bekijken. Laten we eerst breuken omzetten naar decimalen:

Laten we hetzelfde doen met de tweede uitdrukking. De teller van de eerste breuk wordt opnieuw ontbonden:

Er is een belangrijk punt in het derde en vierde voorbeeld: na het wegwerken van de decimale notatie verschijnen er reduceerbare breuken. Deze reductie zullen wij echter niet uitvoeren.

Het laatste voorbeeld is interessant omdat de teller van de tweede breuk een priemgetal bevat. Er valt hier eenvoudigweg niets in factoren te ontbinden, dus beschouwen we het als een rechte lijn:

Soms resulteert deling in een geheel getal (ik heb het over het laatste voorbeeld). In dit geval wordt de derde stap helemaal niet uitgevoerd.

Bovendien ontstaan ​​bij het delen vaak ‘lelijke’ breuken die niet naar decimalen kunnen worden omgezet. Dit onderscheidt delen van vermenigvuldigen, waarbij de resultaten altijd in decimale vorm worden weergegeven. Uiteraard wordt in dit geval de laatste stap opnieuw niet uitgevoerd.

Let ook op het 3e en 4e voorbeeld. Daarin verminderen we opzettelijk de gewone breuken verkregen uit decimalen niet. Anders zal dit de omgekeerde taak bemoeilijken: het uiteindelijke antwoord opnieuw in decimale vorm weergeven.

Onthoud: de basiseigenschap van een breuk (zoals elke andere regel in de wiskunde) betekent op zichzelf niet dat deze overal en altijd, bij elke gelegenheid, moet worden toegepast.

In deze tutorial zullen we elk van deze bewerkingen afzonderlijk bekijken.

Decimalen toevoegen

Zoals we weten bestaat een decimale breuk uit een geheel getal en een breukgedeelte. Bij het optellen van decimalen worden de gehele en gebroken delen afzonderlijk opgeteld.

Laten we bijvoorbeeld de decimale breuken 3.2 en 5.3 optellen. Het is handiger om decimale breuken in een kolom toe te voegen.

Laten we deze twee breuken eerst in een kolom schrijven, waarbij de gehele delen noodzakelijkerwijs onder de gehele getallen staan, en de breuken onder de breuken. Op school heet deze eis "komma onder komma".

Laten we de breuken in een kolom schrijven, zodat de komma onder de komma staat:

We beginnen de fractionele delen toe te voegen: 2 + 3 = 5. We schrijven de vijf in het fractionele deel van ons antwoord:

Nu tellen we de hele delen bij elkaar op: 3 + 5 = 8. We schrijven een acht in het hele deel van ons antwoord:

Nu scheiden we het hele deel van het fractionele deel met een komma. Om dit te doen, volgen we opnieuw de regel "komma onder komma":

Wij kregen als antwoord een 8,5. Dus de uitdrukking 3,2 + 5,3 is gelijk aan 8,5

In feite is niet alles zo eenvoudig als het op het eerste gezicht lijkt. Er zijn hier ook valkuilen, waar we het nu over zullen hebben.

Plaatsen in decimalen

Decimale breuken hebben, net als gewone getallen, hun eigen cijfers. Dit zijn plaatsen van tienden, plaatsen van honderdsten, plaatsen van duizendsten. In dit geval beginnen de cijfers na de komma.

Het eerste cijfer na de komma is verantwoordelijk voor de tienden, het tweede cijfer na de komma voor de honderdsten en het derde cijfer na de komma voor de duizendsten.

Plaatsen in decimale breuken bevatten enkele nuttige informatie. Concreet vertellen ze je hoeveel tienden, honderdsten en duizendsten er in een decimaal staan.

Neem bijvoorbeeld de decimale breuk 0,345

De positie waar de drie zich bevinden wordt genoemd tiende plaats

De positie waar de vier zich bevindt, wordt genoemd honderdste plaats

De positie waar de vijf zich bevindt, wordt genoemd duizendste plaats

Laten we naar deze tekening kijken. We zien dat er een drie op de tiende plaats staat. Dit vertelt ons dat er drie tienden in de decimale breuk 0,345 zitten.

Als we de breuken optellen, krijgen we de oorspronkelijke decimale breuk 0,345

Het is duidelijk dat we eerst het antwoord ontvingen, maar we converteerden het naar een decimale breuk en kregen 0,345.

Bij het optellen van decimale breuken worden dezelfde principes en regels gevolgd als bij het optellen van gewone getallen. Het optellen van decimale breuken gebeurt in cijfers: tienden worden opgeteld bij tienden, honderdsten bij honderdsten, duizendsten bij duizendsten.

Daarom moet u bij het toevoegen van decimale breuken de regel volgen "komma onder komma". De komma onder de komma geeft de volgorde aan waarin tienden worden opgeteld bij tienden, honderdsten bij honderdsten, duizendsten bij duizendsten.

Voorbeeld 1. Zoek de waarde van de uitdrukking 1,5 + 3,4

Allereerst tellen we de breukdelen 5 + 4 = 9 op. In het breukdeel van ons antwoord schrijven we negen:

Nu tellen we de gehele delen 1 + 3 = 4 op. We schrijven de vier in het gehele deel van ons antwoord:

Nu scheiden we het hele deel van het fractionele deel met een komma. Om dit te doen, volgen we opnieuw de regel ‘komma onder komma’:

Wij kregen een antwoord van 4,9. Dit betekent dat de waarde van de uitdrukking 1,5 + 3,4 4,9 is

Voorbeeld 2. Zoek de waarde van de uitdrukking: 3,51 + 1,22

We schrijven deze uitdrukking in een kolom, waarbij we de regel ‘komma onder komma’ in acht nemen.

Allereerst tellen we het breukdeel op, namelijk de honderdsten van 1+2=3. We schrijven een drietal in het honderdste deel van ons antwoord:

Voeg nu de tienden 5+2=7 toe. In het tiende deel van ons antwoord schrijven we een zeven:

Nu tellen we de hele delen 3+1=4 op. We schrijven de vier in het hele deel van ons antwoord:

We scheiden het hele deel van het gedeeltelijke deel met een komma, waarbij we de regel ‘komma onder komma’ in acht nemen:

Het antwoord dat wij kregen was 4,73. Dit betekent dat de waarde van de uitdrukking 3,51 + 1,22 gelijk is aan 4,73

3,51 + 1,22 = 4,73

Net als bij gewone getallen, geldt bij het toevoegen van decimalen . In dit geval wordt één cijfer in het antwoord geschreven en de rest wordt overgebracht naar het volgende cijfer.

Voorbeeld 3. Zoek de waarde van de uitdrukking 2,65 + 3,27

We schrijven deze uitdrukking in de kolom:

Voeg de honderdste delen 5+7=12 toe. Het getal 12 past niet in het honderdste deel van ons antwoord. Daarom schrijven we in het honderdste deel het getal 2 en verplaatsen we de eenheid naar het volgende cijfer:

Nu voegen we de tienden van 6+2=8 toe plus de eenheid die we uit de vorige bewerking kregen, we krijgen 9. We schrijven het getal 9 in de tiende van ons antwoord:

Nu tellen we de hele delen 2+3=5 op. We schrijven het getal 5 in het gehele deel van ons antwoord:

Het antwoord dat wij kregen was 5,92. Dit betekent dat de waarde van de uitdrukking 2,65 + 3,27 gelijk is aan 5,92

2,65 + 3,27 = 5,92

Voorbeeld 4. Zoek de waarde van de uitdrukking 9,5 + 2,8

We schrijven deze uitdrukking in de kolom

We voegen de breukdelen 5 + 8 = 13 toe. Het getal 13 past niet in het breukdeel van ons antwoord, dus schrijven we eerst het getal 3 op en verplaatsen de eenheid naar het volgende cijfer, of beter gezegd, brengen het over naar het geheel getal:

Nu voegen we de gehele delen 9+2=11 toe plus de eenheid die we uit de vorige bewerking kregen, we krijgen 12. We schrijven het getal 12 in het gehele deel van ons antwoord:

Scheid het hele deel van het fractionele deel met een komma:

Wij ontvingen het antwoord 12.3. Dit betekent dat de waarde van de uitdrukking 9,5 + 2,8 12,3 is

9,5 + 2,8 = 12,3

Bij het optellen van decimalen moet het aantal cijfers na de komma in beide breuken hetzelfde zijn. Als er niet genoeg getallen zijn, worden deze plaatsen in het fractionele deel gevuld met nullen.

Voorbeeld 5. Zoek de waarde van de uitdrukking: 12,725 + 1,7

Voordat we deze uitdrukking in een kolom schrijven, moeten we ervoor zorgen dat het aantal cijfers achter de komma in beide breuken hetzelfde is. De decimale breuk 12,725 heeft drie cijfers achter de komma, maar de breuk 1,7 heeft er maar één. Dit betekent dat je in de breuk 1,7 aan het einde twee nullen moet toevoegen. Dan krijgen we de breuk 1.700. Nu kunt u deze uitdrukking in een kolom schrijven en beginnen met berekenen:

Voeg de duizendste delen toe 5+0=5. We schrijven het getal 5 in het duizendste deel van ons antwoord:

Voeg de honderdste delen toe 2+0=2. We schrijven het getal 2 in het honderdste deel van ons antwoord:

Voeg de tienden 7+7=14 toe. Het getal 14 past niet in een tiende van ons antwoord. Daarom noteren we eerst het getal 4 en verplaatsen we de eenheid naar het volgende cijfer:

Nu voegen we de gehele delen 12+1=13 toe plus de eenheid die we uit de vorige bewerking kregen, we krijgen 14. We schrijven het getal 14 in het gehele deel van ons antwoord:

Scheid het hele deel van het fractionele deel met een komma:

We ontvingen een reactie van 14.425. Dit betekent dat de waarde van de uitdrukking 12.725+1.700 14.425 is

12,725+ 1,700 = 14,425

Decimalen aftrekken

Bij het aftrekken van decimale breuken moet u dezelfde regels volgen als bij het optellen: ‘komma onder de komma’ en ‘gelijk aantal cijfers na de komma’.

Voorbeeld 1. Zoek de waarde van de uitdrukking 2,5 − 2,2

We schrijven deze uitdrukking in een kolom, waarbij we de regel ‘komma onder komma’ in acht nemen:

We berekenen het fractionele deel 5−2=3. Het getal 3 schrijven we in het tiende deel van ons antwoord:

We berekenen het gehele deel 2−2=0. We schrijven nul in het gehele deel van ons antwoord:

Scheid het hele deel van het fractionele deel met een komma:

Wij kregen een antwoord van 0,3. Dit betekent dat de waarde van de uitdrukking 2,5 − 2,2 gelijk is aan 0,3

2,5 − 2,2 = 0,3

Voorbeeld 2. Zoek de waarde van de uitdrukking 7.353 - 3.1

Deze uitdrukking heeft een verschillend aantal decimalen. De breuk 7.353 heeft drie cijfers achter de komma, maar de breuk 3.1 heeft er maar één. Dit betekent dat je in breuk 3.1 aan het eind twee nullen moet toevoegen om het aantal cijfers in beide breuken hetzelfde te maken. Dan krijgen we 3.100.

Nu kunt u deze uitdrukking in een kolom schrijven en berekenen:

We ontvingen een reactie van 4.253. Dit betekent dat de waarde van de uitdrukking 7,353 − 3,1 gelijk is aan 4,253

7,353 — 3,1 = 4,253

Net als bij gewone getallen zul je soms een getal van een aangrenzend cijfer moeten lenen als aftrekken onmogelijk wordt.

Voorbeeld 3. Zoek de waarde van de uitdrukking 3,46 − 2,39

Trek honderdsten van 6−9 af. Je kunt het getal 9 niet aftrekken van het getal 6. Daarom moet je er een lenen van het aangrenzende cijfer. Door er één te lenen van het aangrenzende cijfer, verandert het getal 6 in het getal 16. Nu kun je de honderdsten van 16−9=7 berekenen. We schrijven een zeven in het honderdste deel van ons antwoord:

Nu trekken we tienden af. Omdat we één eenheid op de tiende plaats hadden ingenomen, daalde het cijfer dat daar stond met één eenheid. Met andere woorden, op de plaats van de tienden staat nu niet het getal 4, maar het getal 3. Laten we de tienden van 3−3=0 berekenen. In het tiende deel van ons antwoord schrijven we nul:

Nu trekken we de hele delen af ​​3−2=1. We schrijven er één in het gehele deel van ons antwoord:

Scheid het hele deel van het fractionele deel met een komma:

We kregen een antwoord van 1,07. Dit betekent dat de waarde van de uitdrukking 3,46−2,39 gelijk is aan 1,07

3,46−2,39=1,07

Voorbeeld 4. Zoek de waarde van de uitdrukking 3−1.2

In dit voorbeeld wordt een decimaalteken afgetrokken van een geheel getal. Laten we deze uitdrukking in een kolom schrijven, zodat het hele deel van de decimale breuk 1,23 onder het getal 3 staat

Laten we nu het aantal cijfers na de komma hetzelfde maken. Om dit te doen, plaatsen we na het getal 3 een komma en voegen we een nul toe:

Nu trekken we tienden af: 0−2. Je kunt het getal 2 niet van nul aftrekken. Daarom moet je er één lenen van het aangrenzende cijfer. Nadat je er één hebt geleend van het aangrenzende cijfer, verandert 0 in het getal 10. Nu kun je de tienden van 10−2=8 berekenen. In het tiende deel van ons antwoord schrijven we een acht:

Nu trekken we de hele delen af. Voorheen bevond zich nummer 3 in het geheel, maar daar hebben we één eenheid uit gehaald. Als gevolg hiervan veranderde het in het getal 2. Daarom trekken we van 2 1 af. 2−1=1. We schrijven er één in het gehele deel van ons antwoord:

Scheid het hele deel van het fractionele deel met een komma:

Het antwoord dat wij kregen was 1,8. Dit betekent dat de waarde van de uitdrukking 3−1.2 1,8 is

Decimalen vermenigvuldigen

Het vermenigvuldigen van decimalen is eenvoudig en zelfs leuk. Om decimalen te vermenigvuldigen, vermenigvuldig je ze als gewone getallen, waarbij je de komma's negeert.

Nadat je het antwoord hebt ontvangen, moet je het hele deel van het fractionele deel scheiden met een komma. Om dit te doen, moet je het aantal cijfers achter de komma in beide breuken tellen, vervolgens hetzelfde aantal cijfers van rechts in het antwoord tellen en een komma plaatsen.

Voorbeeld 1. Zoek de waarde van de uitdrukking 2,5 × 1,5

Laten we deze decimale breuken vermenigvuldigen als gewone getallen, waarbij we de komma's negeren. Om de komma’s te negeren, kun je je tijdelijk voorstellen dat ze helemaal ontbreken:

We hebben 375. In dit getal moet je het gehele deel van het breukdeel scheiden met een komma. Om dit te doen, moet u het aantal cijfers na de komma in de breuken 2,5 en 1,5 tellen. De eerste breuk heeft één cijfer na de komma, en de tweede breuk heeft er ook één. Totaal twee cijfers.

We keren terug naar nummer 375 en beginnen van rechts naar links te bewegen. We moeten twee cijfers naar rechts tellen en een komma plaatsen:

Wij kregen een antwoord van 3,75. De waarde van de uitdrukking 2,5 × 1,5 is dus 3,75

2,5 × 1,5 = 3,75

Voorbeeld 2. Zoek de waarde van de uitdrukking 12,85 × 2,7

Laten we deze decimale breuken vermenigvuldigen, waarbij we de komma's negeren:

We hebben 34695. In dit getal moet je het gehele deel van het breukdeel scheiden met een komma. Om dit te doen, moet u het aantal cijfers achter de komma in de breuken 12,85 en 2,7 tellen. De breuk 12,85 heeft twee cijfers achter de komma en de breuk 2,7 heeft één cijfer: in totaal drie cijfers.

We keren terug naar het nummer 34695 en beginnen van rechts naar links te bewegen. We moeten drie cijfers naar rechts tellen en een komma plaatsen:

We ontvingen een reactie van 34.695. De waarde van de uitdrukking 12,85 × 2,7 is dus 34,695

12,85 × 2,7 = 34,695

Een decimaal getal vermenigvuldigen met een gewoon getal

Soms doen zich situaties voor waarin u een decimale breuk met een gewoon getal moet vermenigvuldigen.

Om een ​​decimaalteken en een getal te vermenigvuldigen, vermenigvuldig je ze zonder op de komma in het decimaalteken te letten. Nadat je het antwoord hebt ontvangen, moet je het hele deel van het fractionele deel scheiden met een komma. Om dit te doen, moet u het aantal cijfers achter de komma in de decimale breuk tellen, vervolgens hetzelfde aantal cijfers van rechts in het antwoord tellen en een komma plaatsen.

Vermenigvuldig bijvoorbeeld 2,54 met 2

Vermenigvuldig de decimale breuk 2,54 met het gebruikelijke getal 2, negeer de komma:

We hebben het getal 508. In dit getal moet je het gehele deel van het breukdeel scheiden met een komma. Om dit te doen, moet u het aantal cijfers achter de komma in de breuk 2,54 tellen. De breuk 2,54 heeft twee cijfers na de komma.

We keren terug naar nummer 508 en beginnen van rechts naar links te bewegen. We moeten twee cijfers naar rechts tellen en een komma plaatsen:

We kregen een antwoord van 5.08. De waarde van de uitdrukking 2,54 × 2 is dus 5,08

2,54 × 2 = 5,08

Decimalen vermenigvuldigen met 10, 100, 1000

Het vermenigvuldigen van decimalen met 10, 100 of 1000 gebeurt op dezelfde manier als het vermenigvuldigen van decimalen met gewone getallen. U moet de vermenigvuldiging uitvoeren, zonder op de komma in de decimale breuk te letten, en vervolgens het hele deel van het fractionele deel in het antwoord scheiden, waarbij u van rechts hetzelfde aantal cijfers telt als er cijfers na de komma waren.

Vermenigvuldig bijvoorbeeld 2,88 met 10

Vermenigvuldig de decimale breuk 2,88 met 10, negeer de komma in de decimale breuk:

We hebben 2880. In dit getal moet je het gehele deel van het breukdeel scheiden met een komma. Om dit te doen, moet u het aantal cijfers na de komma in de breuk 2,88 tellen. We zien dat de breuk 2,88 twee cijfers achter de komma heeft.

We keren terug naar het nummer 2880 en beginnen van rechts naar links te bewegen. We moeten twee cijfers naar rechts tellen en een komma plaatsen:

Wij kregen als antwoord 28,80. Laten we de laatste nul weglaten en 28,8 krijgen. Dit betekent dat de waarde van de uitdrukking 2,88×10 28,8 is

2,88 × 10 = 28,8

Er is een tweede manier om decimale breuken met 10, 100, 1000 te vermenigvuldigen. Deze methode is veel eenvoudiger en handiger. Het bestaat uit het verplaatsen van de komma naar rechts met zoveel cijfers als er nullen in de factor staan.

Laten we bijvoorbeeld het vorige voorbeeld 2,88×10 op deze manier oplossen. Zonder enige berekening te maken, kijken we meteen naar de factor 10. We zijn geïnteresseerd in hoeveel nullen daarin staan. We zien dat er één nul in zit. Nu verplaatsen we in de breuk 2,88 de komma één cijfer naar rechts en krijgen we 28,8.

2,88 × 10 = 28,8

Laten we proberen 2,88 met 100 te vermenigvuldigen. We kijken meteen naar de factor 100. We zijn geïnteresseerd in hoeveel nullen er in zitten. We zien dat er twee nullen in staan. Nu verplaatsen we in de breuk 2,88 de komma twee cijfers naar rechts, we krijgen 288

2,88 × 100 = 288

Laten we proberen 2,88 met 1000 te vermenigvuldigen. We kijken meteen naar de factor 1000. We zijn geïnteresseerd in hoeveel nullen er in zitten. We zien dat er drie nullen in staan. In de breuk 2,88 verplaatsen we de komma drie cijfers naar rechts. Er is daar geen derde cijfer, dus voegen we nog een nul toe. Als resultaat krijgen we 2880.

2,88 × 1000 = 2880

Decimalen vermenigvuldigen met 0,1 0,01 en 0,001

Het vermenigvuldigen van decimalen met 0,1, 0,01 en 0,001 werkt op dezelfde manier als het vermenigvuldigen van een decimaal met een decimaal. Het is noodzakelijk om de breuken te vermenigvuldigen zoals gewone getallen, en een komma in het antwoord te plaatsen, waarbij je evenveel cijfers naar rechts telt als er cijfers achter de komma in beide breuken staan.

Vermenigvuldig bijvoorbeeld 3,25 met 0,1

We vermenigvuldigen deze breuken als gewone getallen, waarbij we de komma's negeren:

We hebben 325. In dit getal moet je het gehele deel van het breukdeel scheiden met een komma. Om dit te doen, moet u het aantal cijfers achter de komma in de breuken 3,25 en 0,1 tellen. De breuk 3,25 heeft twee cijfers achter de komma en de breuk 0,1 heeft één cijfer. Totaal drie cijfers.

We keren terug naar nummer 325 en beginnen van rechts naar links te bewegen. We moeten drie cijfers vanaf de rechterkant tellen en een komma plaatsen. Nadat we drie cijfers hebben afgeteld, zien we dat de cijfers op zijn. In dit geval moet u één nul en een komma toevoegen:

Wij kregen een antwoord van 0,325. Dit betekent dat de waarde van de uitdrukking 3,25 × 0,1 0,325 is

3,25 × 0,1 = 0,325

Er is een tweede manier om decimalen te vermenigvuldigen met 0,1, 0,01 en 0,001. Deze methode is veel eenvoudiger en handiger. Het bestaat uit het verplaatsen van de komma naar links met zoveel cijfers als er nullen in de factor staan.

Laten we bijvoorbeeld het vorige voorbeeld 3,25 × 0,1 op deze manier oplossen. Zonder berekeningen te geven, kijken we meteen naar de vermenigvuldiger van 0,1. We zijn geïnteresseerd in hoeveel nullen het bevat. We zien dat er één nul in zit. In de breuk 3,25 verplaatsen we de komma één cijfer naar links. Door de komma één cijfer naar links te verplaatsen, zien we dat er geen cijfers meer vóór de drie staan. Voeg in dit geval één nul toe en plaats een komma. Het resultaat is 0,325

3,25 × 0,1 = 0,325

Laten we proberen 3,25 met 0,01 te vermenigvuldigen. We kijken meteen naar de vermenigvuldiger van 0,01. We zijn geïnteresseerd in hoeveel nullen het bevat. We zien dat er twee nullen in staan. Nu verplaatsen we in de breuk 3,25 de komma twee cijfers naar links, we krijgen 0,0325

3,25 × 0,01 = 0,0325

Laten we proberen 3,25 met 0,001 te vermenigvuldigen. We kijken meteen naar de vermenigvuldiger van 0,001. We zijn geïnteresseerd in hoeveel nullen het bevat. We zien dat er drie nullen in staan. Nu verplaatsen we in de breuk 3,25 de komma drie cijfers naar links, we krijgen 0,00325

3,25 × 0,001 = 0,00325

Verwar het vermenigvuldigen van decimale breuken met 0,1, 0,001 en 0,001 niet met het vermenigvuldigen met 10, 100, 1000. Veel voorkomende fout de meeste mensen.

Bij vermenigvuldigen met 10, 100, 1000 wordt de komma met hetzelfde aantal cijfers naar rechts verplaatst als er nullen in de vermenigvuldiger staan.

En bij vermenigvuldiging met 0,1, 0,01 en 0,001 wordt de komma met hetzelfde aantal cijfers naar links verplaatst als er nullen in de vermenigvuldiger staan.

Als het in eerste instantie moeilijk te onthouden is, kunt u de eerste methode gebruiken, waarbij vermenigvuldiging wordt uitgevoerd zoals bij gewone getallen. In het antwoord moet je het hele deel van het breukdeel scheiden, door hetzelfde aantal cijfers aan de rechterkant te tellen als er cijfers achter de komma in beide breuken staan.

Een kleiner getal delen door een groter getal. Gevorderd niveau.

In een van de vorige lessen hebben we gezegd dat wanneer je een kleiner getal deelt door een groter getal, je een breuk krijgt, waarvan de teller het deeltal is en de noemer de deler.

Als u bijvoorbeeld één appel onder twee mensen wilt verdelen, moet u 1 (één appel) in de teller schrijven en 2 (twee vrienden) in de noemer. Als resultaat krijgen we de breuk . Dit betekent dat elke vriend een appel krijgt. Met andere woorden: een halve appel. De breuk is het antwoord op het probleem “hoe verdeel je een appel in twee”

Het blijkt dat je dit probleem verder kunt oplossen als je 1 door 2 deelt. De breuklijn in elke breuk betekent immers deling, en daarom is deze deling toegestaan ​​in de breuk. Maar hoe? We zijn eraan gewend dat het deeltal altijd groter is dan de deler. Maar hier is het deeltal daarentegen kleiner dan de deler.

Alles zal duidelijk worden als we bedenken dat een breuk verplettering, verdeeldheid, verdeeldheid betekent. Dit betekent dat de unit in zoveel delen kan worden gesplitst als gewenst, en niet slechts in twee delen.

Wanneer je een kleiner getal deelt door een groter getal, krijg je een decimale breuk waarvan het gehele deel 0 (nul) is. Het fractionele deel kan van alles zijn.

Laten we dus 1 door 2 delen. Laten we dit voorbeeld oplossen met een hoek:

Men kan niet volledig in tweeën worden verdeeld. Als je een vraag stelt “hoeveel tweeën zijn er in één” , dan is het antwoord 0. Daarom schrijven we in het quotiënt 0 en plaatsen we een komma:

Nu vermenigvuldigen we, zoals gewoonlijk, het quotiënt met de deler om de rest te krijgen:

Het moment is aangebroken waarop de eenheid in twee delen kan worden gesplitst. Om dit te doen, voegt u nog een nul toe rechts van de resulterende nul:

We hebben 10. Deel 10 door 2 en we krijgen 5. We schrijven de vijf in het breukdeel van ons antwoord:

Nu halen we het laatste restant eruit om de berekening te voltooien. Vermenigvuldig 5 met 2 om 10 te krijgen

Wij kregen een antwoord van 0,5. De breuk is dus 0,5

Een halve appel kan ook worden geschreven met de decimale breuk 0,5. Als we deze twee helften (0,5 en 0,5) bij elkaar optellen, krijgen we weer de originele hele appel:

Dit punt kan ook worden begrepen als je je voorstelt hoe 1 cm in twee delen is verdeeld. Als je 1 centimeter in 2 delen verdeelt, krijg je 0,5 cm

Voorbeeld 2. Zoek de waarde van de uitdrukking 4:5

Hoeveel vijven zitten er in een vier? Helemaal niet. We schrijven 0 in het quotiënt en plaatsen een komma:

We vermenigvuldigen 0 met 5, we krijgen 0. We schrijven een nul onder de vier. Trek deze nul onmiddellijk af van het dividend:

Laten we nu beginnen met het splitsen (verdelen) van de vier in vijf delen. Voeg hiervoor een nul toe rechts van 4 en deel 40 door 5, we krijgen 8. We schrijven acht in het quotiënt.

We voltooien het voorbeeld door 8 met 5 te vermenigvuldigen om 40 te krijgen:

Wij kregen een antwoord van 0,8. Dit betekent dat de waarde van de uitdrukking 4:5 0,8 is

Voorbeeld 3. Zoek de waarde van uitdrukking 5: 125

Hoeveel getallen zijn 125 in vijf? Helemaal niet. We schrijven 0 in het quotiënt en plaatsen een komma:

We vermenigvuldigen 0 met 5, we krijgen 0. We schrijven 0 onder de vijf. Trek onmiddellijk 0 af van vijf

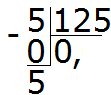
Laten we nu beginnen met het splitsen (verdelen) van de vijf in 125 delen. Om dit te doen, schrijven we een nul rechts van deze vijf:

Deel 50 door 125. Hoeveel getallen zijn 125 in het getal 50? Helemaal niet. Dus in het quotiënt schrijven we weer 0

Vermenigvuldig 0 met 125, we krijgen 0. Schrijf deze nul onder 50. Trek onmiddellijk 0 af van 50

Verdeel nu het getal 50 in 125 delen. Om dit te doen, schrijven we nog een nul rechts van 50:

Deel 500 door 125. Hoeveel getallen zijn 125 in het getal 500? Er zijn vier getallen 125 in het getal 500. Schrijf de vier in het quotiënt:

We voltooien het voorbeeld door 4 te vermenigvuldigen met 125 om 500 te krijgen

Wij kregen een antwoord van 0,04. Dit betekent dat de waarde van uitdrukking 5: 125 0,04 is

Getallen delen zonder rest

Laten we dus een komma achter de eenheid in het quotiënt plaatsen, waarmee we aangeven dat de deling van gehele delen voorbij is en we doorgaan naar het fractionele deel:

Laten we nul optellen bij de rest 4

Deel nu 40 door 5, we krijgen 8. We schrijven acht in het quotiënt:

40−40=0. Wij hebben er nog 0 over. Dit betekent dat de splitsing volledig is afgerond. Het delen van 9 door 5 geeft de decimale breuk 1,8:

9: 5 = 1,8

Voorbeeld 2. Verdeel 84 door 5 zonder rest

Deel eerst 84 door 5 zoals gebruikelijk met een rest:

We hebben er 16 privé en nog 4 over. Laten we deze rest nu delen door 5. Zet een komma in het quotiënt en tel 0 op bij de rest 4

Nu delen we 40 door 5, we krijgen 8. We schrijven de acht in het quotiënt achter de komma:

en vervolledig het voorbeeld door te controleren of er nog een rest is:

Een decimaal delen door een gewoon getal

Een decimale breuk bestaat, zoals we weten, uit een geheel getal en een breukgedeelte. Wanneer u een decimale breuk deelt door een gewoon getal, moet u eerst:

• deel het hele deel van de decimale breuk door dit getal;
• nadat het hele deel is verdeeld, moet je onmiddellijk een komma in het quotiënt plaatsen en doorgaan met de berekening, zoals bij een normale deling.

Deel bijvoorbeeld 4,8 door 2

Laten we dit voorbeeld in een hoek schrijven:

Laten we nu het hele deel door 2 delen. Vier gedeeld door twee is gelijk aan twee. We schrijven er twee in het quotiënt en plaatsen onmiddellijk een komma:

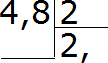
Nu vermenigvuldigen we het quotiënt met de deler en kijken of er een rest overblijft van de deling:

4−4=0. Rest gelijk aan nul. We schrijven nog geen nul, omdat de oplossing nog niet is voltooid. Vervolgens gaan we verder met berekenen zoals bij een gewone deling. Neem 8 af en deel het door 2

8: 2 = 4. We schrijven de vier in het quotiënt en vermenigvuldigen dit onmiddellijk met de deler:

Wij kregen een antwoord van 2,4. De waarde van de uitdrukking 4,8:2 is 2,4

Voorbeeld 2. Zoek de waarde van de uitdrukking 8.43: 3

Deel 8 door 3, we krijgen 2. Zet onmiddellijk een komma na de 2:

Nu vermenigvuldigen we het quotiënt met de deler 2 × 3 = 6. We schrijven de zes onder de acht en vinden de rest:

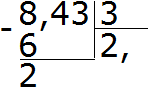
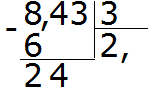
Deel 24 door 3, we krijgen 8. We schrijven acht in het quotiënt. Vermenigvuldig het onmiddellijk met de deler om de rest van de deling te vinden:

24−24=0. De rest is nul. We schrijven nog geen nul op. We halen de laatste drie weg uit het deeltal en delen door 3, we krijgen 1. Vermenigvuldig onmiddellijk 1 met 3 om dit voorbeeld compleet te maken:

Het antwoord dat wij kregen was 2,81. Dit betekent dat de waarde van de uitdrukking 8.43:3 2,81 is

Een decimaal delen door een decimaal

Om een ​​decimale breuk te delen door een decimale breuk, moet u de komma in het deeltal en de deler naar rechts verplaatsen met hetzelfde aantal cijfers als er na de komma in de deler staan, en vervolgens delen door het gebruikelijke getal.

Deel bijvoorbeeld 5,95 door 1,7

Laten we deze uitdrukking met een hoek schrijven

Nu verplaatsen we in het deeltal en in de deler de komma naar rechts met hetzelfde aantal cijfers als er na de komma in de deler staan. De deler heeft één cijfer na de komma. Dit betekent dat we in het deeltal en de deler de komma één cijfer naar rechts moeten verplaatsen. Wij maken over:

Nadat de komma één cijfer naar rechts was verplaatst, werd de decimale breuk 5,95 de breuk 59,5. En de decimale breuk 1,7 veranderde, nadat de komma één cijfer naar rechts was verplaatst, in het gebruikelijke getal 17. En we weten al hoe we een decimale breuk door een gewoon getal moeten delen. Verdere berekening is niet moeilijk:

De komma is naar rechts verplaatst om de verdeling gemakkelijker te maken. Dit is toegestaan ​​omdat bij het vermenigvuldigen of delen van het deeltal en de deler door hetzelfde getal het quotiënt niet verandert. Wat betekent het?

Dit is er één van interessante kenmerken divisie. Dit wordt de quotiënteigenschap genoemd. Beschouw uitdrukking 9: 3 = 3. Als in deze uitdrukking het deeltal en de deler worden vermenigvuldigd of gedeeld door hetzelfde getal, verandert het quotiënt 3 niet.

Laten we het deeltal en de deler met 2 vermenigvuldigen en kijken wat eruit komt:

(9 × 2): (3 × 2) = 18: 6 = 3

Zoals uit het voorbeeld blijkt, is het quotiënt niet veranderd.

Hetzelfde gebeurt als we de komma in het deeltal en in de deler verplaatsen. In het vorige voorbeeld, waar we 5,91 door 1,7 deelden, hebben we de komma in het deeltal en de deler één cijfer naar rechts verplaatst. Na het verplaatsen van de komma werd de breuk 5,91 omgezet in de breuk 59,1 en de breuk 1,7 werd omgezet in het gebruikelijke getal 17.

In feite was er binnen dit proces een vermenigvuldiging met 10. Zo zag het eruit:

5,91 × 10 = 59,1

Daarom bepaalt het aantal cijfers achter de komma in de deler waarmee het deeltal en de deler worden vermenigvuldigd. Met andere woorden, het aantal cijfers achter de komma in de deler bepaalt hoeveel cijfers in het deeltal en in de deler de komma naar rechts wordt verplaatst.

Een decimaal delen door 10, 100, 1000

Het delen van een decimaal door 10, 100 of 1000 gaat op dezelfde manier als . Deel bijvoorbeeld 2,1 door 10. Los dit voorbeeld op met een hoek:

Maar er is een tweede manier. Het is lichter. De essentie van deze methode is dat de komma in het deeltal evenveel cijfers naar links wordt verplaatst als er nullen in de deler staan.

Laten we het vorige voorbeeld op deze manier oplossen. 2.1: 10. We kijken naar de deler. We zijn geïnteresseerd in hoeveel nullen het bevat. We zien dat er één nul is. Dit betekent dat je bij het deeltal 2,1 de komma één cijfer naar links moet verplaatsen. We verplaatsen de komma één cijfer naar links en zien dat er geen cijfers meer over zijn. Voeg in dit geval nog een nul toe vóór het getal. Als resultaat krijgen we 0,21

Laten we proberen 2,1 door 100 te delen. Er zijn twee nullen in 100. Dit betekent dat we in deeltal 2.1 de komma twee cijfers naar links moeten verplaatsen:

2,1: 100 = 0,021

Laten we proberen 2,1 te delen door 1000. Er zijn drie nullen in 1000. Dit betekent dat je in deeldeel 2.1 de komma drie cijfers naar links moet verplaatsen:

2,1: 1000 = 0,0021

Een decimaal delen door 0,1, 0,01 en 0,001

Het delen van een decimale breuk door 0,1, 0,01 en 0,001 gebeurt op dezelfde manier als . In het deeltal en in de deler moet u de komma met net zoveel cijfers naar rechts verplaatsen als er na de komma in de deler staan.

Laten we bijvoorbeeld 6,3 delen door 0,1. Laten we eerst de komma's in het deeltal en de deler naar rechts verplaatsen met hetzelfde aantal cijfers als er achter de komma in de deler staan. De deler heeft één cijfer na de komma. Dit betekent dat we de komma's in het deeltal en de deler één cijfer naar rechts verplaatsen.

Nadat de komma één cijfer naar rechts is verplaatst, wordt de decimale breuk 6,3 het gebruikelijke getal 63, en de decimale breuk 0,1 verandert na het verplaatsen van de komma één cijfer naar rechts in één. En het delen van 63 door 1 is heel eenvoudig:

Dit betekent dat de waarde van de uitdrukking 6.3: 0.1 63 is

Maar er is een tweede manier. Het is lichter. De essentie van deze methode is dat de komma in het deeltal evenveel cijfers naar rechts wordt verplaatst als er nullen in de deler staan.

Laten we het vorige voorbeeld op deze manier oplossen. 6,3: 0,1. Laten we naar de deler kijken. We zijn geïnteresseerd in hoeveel nullen het bevat. We zien dat er één nul is. Dit betekent dat je bij het deeltal 6,3 de komma één cijfer naar rechts moet verplaatsen. Verplaats de komma één cijfer naar rechts en je krijgt 63

Laten we proberen 6,3 te delen door 0,01. De deler van 0,01 heeft twee nullen. Dit betekent dat we in deeltal 6.3 de komma twee cijfers naar rechts moeten verplaatsen. Maar in het deeltal staat slechts één cijfer achter de komma. In dit geval moet u aan het einde nog een nul toevoegen. Als resultaat krijgen we 630

Laten we proberen 6,3 te delen door 0,001. De deler van 0,001 heeft drie nullen. Dit betekent dat we in deeltal 6.3 de komma drie cijfers naar rechts moeten verplaatsen:

6,3: 0,001 = 6300

Taken voor onafhankelijke oplossing

Vond je de les leuk?
Sluit je aan bij onze nieuwe groep VKontakte en ontvang meldingen over nieuwe lessen

Laten we naar specifieke voorbeelden kijken om te begrijpen hoe u decimalen kunt vermenigvuldigen.

Regel voor het vermenigvuldigen van decimalen

1) Vermenigvuldig zonder op de komma te letten.

2) Als gevolg hiervan scheiden we in beide factoren samen evenveel cijfers na de komma als er na de komma zijn.

Voorbeelden.

Zoek het product van decimale breuken:

Om decimale breuken te vermenigvuldigen, vermenigvuldigen we zonder op komma's te letten. Dat wil zeggen, we vermenigvuldigen niet 6,8 en 3,4, maar 68 en 34. Het resultaat is dat we in beide factoren samen evenveel cijfers na de komma scheiden als er na de komma zijn. In de eerste factor staat één cijfer achter de komma, in de tweede is er ook één. In totaal scheiden we twee getallen achter de komma. Zo kregen we het uiteindelijke antwoord: 6,8∙3,4=23,12.

We vermenigvuldigen decimalen zonder rekening te houden met de komma. Dat wil zeggen dat we in plaats van 36,85 met 1,14 te vermenigvuldigen, 3685 met 14 vermenigvuldigen. We krijgen 51590. In dit resultaat moeten we nu zoveel cijfers met een komma scheiden als er in beide factoren samen zijn. Het eerste getal heeft twee cijfers na de komma, het tweede heeft er één. In totaal scheiden we drie cijfers met een komma. Omdat er aan het einde van de invoer een nul achter de komma staat, schrijven we deze niet in het antwoord: 36,85∙1,4=51,59.

Om deze decimalen te vermenigvuldigen, vermenigvuldigen we de getallen zonder op de komma's te letten. Dat wil zeggen, we vermenigvuldigen de natuurlijke getallen 2315 en 7. We krijgen 16205. In dit getal moet je vier cijfers na de komma scheiden - zoveel als er in beide factoren samen zijn (twee in elk). Eindantwoord: 23,15∙0,07=1,6205.

Het vermenigvuldigen van een decimale breuk met een natuurlijk getal gaat op dezelfde manier. We vermenigvuldigen de getallen zonder op de komma te letten, dat wil zeggen, we vermenigvuldigen 75 met 16. Het resulterende resultaat moet hetzelfde aantal tekens achter de komma bevatten als in beide factoren samen: één. Dus 75∙1,6=120,0=120.

We beginnen met het vermenigvuldigen van decimale breuken door natuurlijke getallen te vermenigvuldigen, omdat we geen aandacht besteden aan komma's. Hierna scheiden we zoveel cijfers achter de komma als er in beide factoren samen zijn. Het eerste getal heeft twee decimalen, het tweede ook twee. In totaal moet het resultaat vier cijfers na de komma zijn: 4,72∙5,04=23,7888.

Het decimaalteken wordt gebruikt wanneer u bewerkingen moet uitvoeren op niet-gehele getallen. Dit lijkt misschien irrationeel. Maar dit soort getallen vereenvoudigt de wiskundige bewerkingen die ermee moeten worden uitgevoerd aanzienlijk. Dit begrip komt in de loop van de tijd, wanneer het schrijven ervan vertrouwd wordt, en het lezen ervan geen problemen oplevert, en de regels van decimale breuken onder de knie zijn. Bovendien herhalen alle acties reeds bekende acties, die met natuurlijke getallen zijn geleerd. U hoeft alleen maar enkele functies te onthouden.

Decimale definitie

Een decimaal is een speciale weergave van een niet-geheel getal met een noemer die deelbaar is door 10, waardoor het antwoord één en mogelijk nullen is. Met andere woorden: als de noemer 10, 100, 1000, enzovoort is, is het handiger om het getal te herschrijven met een komma. Vervolgens wordt het hele deel ervoor geplaatst, en vervolgens het fractionele deel. Bovendien zal de opname van de tweede helft van het getal afhangen van de noemer. Het aantal cijfers in het breukgedeelte moet gelijk zijn aan het cijfer van de noemer.

Het bovenstaande kan worden geïllustreerd met deze cijfers:

9/10=0,9; 178/10000=0,0178; 3,05; 56 003,7006.

Redenen voor het gebruik van decimalen

Wiskundigen hadden om verschillende redenen decimalen nodig:

Vereenvoudigde opname. Zo'n breuk bevindt zich langs één lijn zonder streepje tussen de noemer en de teller, terwijl de duidelijkheid er niet onder lijdt.

Eenvoud in vergelijking. Het is voldoende om eenvoudigweg getallen te correleren die op dezelfde positie staan, terwijl je ze bij gewone breuken zou moeten herleiden tot een gemeenschappelijke noemer.

Vereenvoudig berekeningen.

Rekenmachines zijn niet ontworpen om breuken te accepteren; ze gebruiken decimale notatie voor alle bewerkingen.

Hoe dergelijke cijfers correct te lezen?

Het antwoord is simpel: net als een gewoon gemengd getal met een noemer die een veelvoud van 10 is. De enige uitzondering zijn breuken zonder een geheel getal. Bij het lezen moet je dan ‘nul gehele getallen’ uitspreken.

45/1000 moet bijvoorbeeld worden uitgesproken als vijfenveertigduizendste, tegelijkertijd zal 0,045 klinken nul komma vijfenveertigduizendsten.

Een gemengd getal met een geheel getal van 7 en een breuk van 17/100, dat zou worden geschreven als 7,17, zou in beide gevallen worden gelezen als zeven komma zeventien.

De rol van cijfers bij het schrijven van breuken

Het correct markeren van de rang is wat wiskunde vereist. Decimalen en hun betekenis kunnen aanzienlijk veranderen als u het cijfer op de verkeerde plaats schrijft. Dit was echter eerder zo.

Om de cijfers van het hele deel van een decimale breuk te lezen, hoeft u alleen maar de bekende regels te gebruiken natuurlijke getallen. En aan de rechterkant worden ze gespiegeld en anders gelezen. Als het hele deel “tienden” klonk, dan zijn het na de komma al “tienden”.

Dit is duidelijk te zien in deze tabel.

Hoe schrijf je een gemengd getal correct als decimaal?

Als de noemer een getal bevat dat gelijk is aan 10 of 100, en andere, dan is de vraag hoe je een breuk naar een decimaal getal kunt converteren niet moeilijk. Om dit te doen, volstaat het om alle componenten anders te herschrijven. De volgende punten helpen hierbij:

schrijf de teller van de breuk een beetje opzij, op dit moment bevindt de komma zich aan de rechterkant, na het laatste cijfer;

verplaats de komma naar links, het belangrijkste hier is om de getallen correct te tellen - je moet deze met zoveel posities verplaatsen als er nullen in de noemer staan;

als er niet genoeg zijn, dan moeten er nullen in de lege posities staan;

de nullen die aan het einde van de teller stonden, zijn nu niet nodig en kunnen worden doorgestreept;

Voeg vóór de komma het hele deel toe; als het er niet was, dan staat hier ook nul.

Aandacht. Nullen die omgeven zijn door andere cijfers, kunt u niet doorstrepen.

Hieronder leest u hoe u omgaat met een situatie waarin de noemer meer dan alleen maar enen en nullen bevat, en hoe u een breuk naar een decimaal getal omzet. Dit belangrijke informatie, die zeker de moeite waard is om te bekijken.

Hoe converteer je een breuk naar een decimaal getal als de noemer een willekeurig getal is?

Er zijn hier twee opties:

Wanneer de noemer kan worden weergegeven als een getal dat gelijk is aan tien tot elke macht.

Als een dergelijke handeling niet kan worden uitgevoerd.

Hoe kan ik dit controleren? Je moet de noemer ontbinden. Als er alleen 2 en 5 in het product voorkomen, is alles in orde en kan de breuk eenvoudig worden omgezet in een laatste decimaal. IN anders Als 3, 7 en andere priemgetallen verschijnen, is het resultaat oneindig. Het is gebruikelijk om een ​​dergelijke decimale breuk af te ronden voor gebruiksgemak bij wiskundige bewerkingen. Dit zal hieronder een beetje worden besproken.

Onderzoekt hoe decimalen worden gemaakt, 5e leerjaar. Voorbeelden hier zullen zeer nuttig zijn.

Laat de noemers de getallen bevatten: 40, 24 en 75. De ontleding in priemfactoren voor hen zal als volgt zijn:

• 40=2·2·2·5;
• 24=2·2·2·3;
• 75=5·5·3.

In deze voorbeelden kan alleen de eerste breuk worden weergegeven als de laatste breuk.

Algoritme voor het omzetten van een gewone breuk naar een einddecimaal

Controleer de factorisatie van de noemer in priemfactoren en zorg ervoor dat deze uit 2 en 5 bestaat.

Voeg zoveel 2-en en 5-en toe aan deze getallen, zodat er een gelijk aantal is. Ze geven de waarde van de extra vermenigvuldiger weer.

Vermenigvuldig de noemer en de teller met dit getal. Het resultaat zal een gewone breuk zijn, onder de lijn waarvan er tot op zekere hoogte 10 is.

Als deze acties in het probleem worden uitgevoerd met een gemengd getal, moet dit eerst worden weergegeven als een onechte breuk. En handel dan pas volgens het beschreven scenario.

Een breuk weergeven als een afgeronde decimaal

Deze methode om een ​​breuk naar een decimaal getal om te zetten, lijkt voor sommigen misschien nog eenvoudiger. Omdat dat niet het geval is grote hoeveelheid acties. Je hoeft alleen maar de teller te delen door de noemer.

Aan elk getal met een decimaal gedeelte rechts van de komma kan een oneindig aantal nullen worden toegewezen. Deze eigenschap is waar u van moet profiteren.

Schrijf eerst het hele gedeelte op en zet er een komma achter. Als de breuk juist is, schrijf dan nul.

Dan moet je de teller delen door de noemer. Zodat ze hetzelfde aantal cijfers hebben. Dat wil zeggen: optellen rechts van de teller benodigde hoeveelheid nullen.

Voer een staartdeling uit totdat het vereiste aantal cijfers is bereikt. Als u bijvoorbeeld moet afronden op honderdsten, dan zou het antwoord 3 moeten zijn. Over het algemeen zou er één getal meer moeten zijn dan u uiteindelijk nodig heeft.

Schrijf het tussenantwoord achter de komma en rond af volgens de regels. Als het laatste cijfer tussen 0 en 4 ligt, hoeft u het alleen maar weg te gooien. En als het gelijk is aan 5-9, dan moet degene ervoor met één worden verhoogd, waarbij de laatste wordt weggegooid.

Terugkeer van decimaal naar gewone breuk

In de wiskunde zijn er problemen wanneer het handiger is om decimale breuken weer te geven in de vorm van gewone breuken, waarin er een teller met een noemer is. U kunt opgelucht ademhalen: deze operatie is altijd mogelijk.

Voor deze procedure moet u het volgende doen:

schrijf het hele deel op, als het gelijk is aan nul, dan hoef je niets te schrijven;

teken een breuklijn;

schrijf erboven de cijfers vanaf de rechterkant op, als de nullen eerst komen, dan moeten ze worden doorgestreept;

Schrijf er onder de regel één met evenveel nullen als er cijfers achter de komma staan ​​in de oorspronkelijke breuk.

Dat is alles wat u hoeft te doen om een ​​decimaal getal naar een breuk om te zetten.

Wat kun je met decimalen?

In de wiskunde zullen dit bepaalde bewerkingen met decimalen zijn die eerder voor andere getallen werden uitgevoerd.

Zij zijn:

vergelijking;

optellen en aftrekken;

vermenigvuldigen en delen.

De eerste actie, vergelijking, is vergelijkbaar met hoe deze voor natuurlijke getallen werd uitgevoerd. Om te bepalen welke groter is, moet je de cijfers van het hele onderdeel vergelijken. Als ze gelijk blijken te zijn, gaan ze verder met de breuk en vergelijken ze ook met cijfers. Het nummer waar het terechtkomt groot aantal in de hogere rang, en zal het antwoord zijn.

Decimalen optellen en aftrekken

Dit zijn misschien wel de eenvoudigste stappen. Omdat ze worden uitgevoerd volgens de regels voor natuurlijke getallen.



Om decimale breuken toe te voegen, moeten ze dus onder elkaar worden geschreven, waarbij komma's in een kolom worden geplaatst. Met deze notatie verschijnen hele delen links van de komma's en gedeeltelijke delen rechts. En nu moet je de getallen beetje bij beetje optellen, zoals bij natuurlijke getallen gebeurt, waarbij je de komma naar beneden verplaatst. U moet beginnen met optellen vanaf het kleinste cijfer van het fractionele deel van het getal. Als er niet genoeg getallen in de rechterhelft staan, worden er nullen toegevoegd.

Hetzelfde geldt voor aftrekken. En hier is er een regel die de mogelijkheid beschrijft om een ​​​​eenheid van de hoogste rang te nemen. Als de breuk die wordt verkleind minder cijfers achter de komma heeft dan de breuk die wordt afgetrokken, worden er eenvoudigweg nullen aan toegevoegd.

De situatie is iets ingewikkelder bij taken waarbij u decimale breuken moet vermenigvuldigen en delen.

Hoe vermenigvuldig je een decimale breuk in verschillende voorbeelden?

De regel voor het vermenigvuldigen van decimale breuken met een natuurlijk getal is:

schrijf ze op in een kolom, negeer de komma;

vermenigvuldigen alsof ze natuurlijk zijn;

Scheid met een komma zoveel cijfers als er in het fractionele deel van het oorspronkelijke getal stonden.

Een speciaal geval is het voorbeeld waarin een natuurlijk getal gelijk is aan 10 tot welke macht dan ook. Om het antwoord te krijgen, hoeft u de komma net zoveel posities naar rechts te verplaatsen als er nullen in de andere factor staan. Met andere woorden: bij vermenigvuldiging met 10 verplaatst de komma zich met één cijfer, met 100 - er zullen er al twee zijn, enzovoort. Als er niet genoeg getallen in het fractionele deel staan, moet je nullen op de lege posities schrijven.

De regel die wordt gebruikt wanneer een taak vereist dat decimale breuken met een ander hetzelfde getal worden vermenigvuldigd:

schrijf ze een voor een op, zonder op komma's te letten;

vermenigvuldigen alsof ze natuurlijk zijn;

Scheid met een komma zoveel cijfers als er in de breukdelen van beide oorspronkelijke breuken samen stonden.

Een speciaal geval zijn voorbeelden waarin een van de vermenigvuldigers gelijk is aan 0,1 of 0,01 enzovoort. Daarin moet je de komma naar links verplaatsen met het aantal cijfers in de gepresenteerde factoren. Dat wil zeggen, als het wordt vermenigvuldigd met 0,1, wordt de komma één positie verschoven.

Hoe verdeel je een decimale breuk in verschillende taken?

Het delen van decimale breuken door een natuurlijk getal gebeurt volgens de volgende regel:

schrijf ze op voor verdeling in een kolom alsof het natuurlijke exemplaren zijn;

verdeel volgens de gebruikelijke regel totdat het hele deel voorbij is;

plaats een komma in het antwoord;

ga door met het delen van de fractionele component totdat de rest nul is;

indien nodig kunt u het vereiste aantal nullen toevoegen.

Als het gehele deel gelijk is aan nul, dan staat dit ook niet in het antwoord.

Afzonderlijk is er een verdeling in getallen gelijk aan tien, honderd, enzovoort. Bij dergelijke problemen moet u de komma naar links verplaatsen met het aantal nullen in de deler. Het komt voor dat er niet genoeg getallen in een heel deel staan, dan worden in plaats daarvan nullen gebruikt. U kunt zien dat deze bewerking vergelijkbaar is met vermenigvuldigen met 0,1 en soortgelijke getallen.

Om decimalen te delen, moet je deze regel gebruiken:

verander de deler in een natuurlijk getal en verplaats hiervoor de komma naar rechts tot aan het einde;

verplaats de komma in het deeltal met hetzelfde aantal cijfers;

handel volgens het vorige scenario.

De deling door 0,1 is gemarkeerd; 0,01 en andere soortgelijke cijfers. In dergelijke voorbeelden wordt de komma naar rechts verschoven met het aantal cijfers in het breukgedeelte. Als ze op zijn, moet je het ontbrekende aantal nullen toevoegen. Het is vermeldenswaard dat deze actie de deling door 10 en soortgelijke getallen herhaalt.



Conclusie: het draait allemaal om oefenen

Niets bij het leren gaat gemakkelijk of zonder inspanning. Het betrouwbaar beheersen van nieuw materiaal kost tijd en oefening. Wiskunde is geen uitzondering.

Om ervoor te zorgen dat het onderwerp over decimale breuken geen problemen oplevert, moet je er zoveel mogelijk voorbeelden mee oplossen. Er was tenslotte een tijd dat het toevoegen van natuurlijke getallen een doodlopende weg was. En nu is alles in orde.

Daarom, om te parafraseren beroemde zin: beslissen, beslissen en nog eens beslissen. Dan worden taken met dergelijke cijfers gemakkelijk en natuurlijk voltooid, als een nieuwe puzzel.

Trouwens, puzzels zijn in het begin moeilijk op te lossen, en dan moet je de gebruikelijke bewegingen uitvoeren. Hetzelfde binnen wiskundige voorbeelden: Als je meerdere keren hetzelfde pad hebt bewandeld, denk je niet meer na over waar je heen moet.

1 les

1. Organisatorisch moment

Controleer of de leerlingen klaar zijn voor de les.

(Beschikbaarheid van educatieve benodigdheden voor de les)

I . Kennis bijwerken

Mondeling werk.

Doel: Systematiseer de voorkennis die nodig is bij het leren van nieuw materiaal.

De leerlingen voeren mondeling opdrachten uit over het vermenigvuldigen van een decimale breuk met een natuurlijk getal en het vermenigvuldigen van gewone breuken.

Berekenen:

Vervolgens stelt de leraar de vraag: Formuleer hoe je een decimale breuk vermenigvuldigt met een natuurlijk getal. De leerlingen onthouden de definitie. Het onderwerp van de les en de doelen van de les worden gerapporteerd.

II .Gelijktijdige indeling in groepen en paren.

De leerlingen kiezen één kaart uit de tafel van de leraar. Sommige bevatten voorbeelden van bewerkingen met gewone breuken, en andere bevatten de bijbehorende antwoorden. Ze zullen overeenkomsten moeten vinden en worden in paren verdeeld. Als ze in groepen werken, worden ze op deze manier verdeeld:

Groep 1 zijn de leerlingen die voorbeelden zijn tegengekomen, groep 2 zijn de leerlingen die de juiste antwoorden hebben (zie bijlage nr. 1).

III .Nieuw materiaal leren

Doel: Laat leerlingen kennismaken met nieuw materiaal.

Uitleg van de leraar:

3.1.Groepswerk.

Doel: Nadat je het probleem op twee manieren onafhankelijk hebt opgelost, formuleer je de regel voor het vermenigvuldigen van een decimale breuk met een decimale breuk.

De leerlingen krijgen de volgende opdracht:

De lengte van de rechthoek is 6,3 cm, breedte 2,8 cm. Vind het gebied.

Elke groep voltooit deze taak volgens de voorgestelde methode die haar wordt aangegeven.

Methode 1: Schrijf op numerieke waarden afmetingen van een rechthoek in de vorm van natuurlijke getallen, uitgedrukt in millimeters. Bereken de oppervlakte en druk het resulterende antwoord uit in vierkante centimeters.

Methode 2: Geef de afmetingen van een rechthoek weer in de vorm van gewone breuken, vind het gebied door te vermenigvuldigen gewone breuken en omzetten naar een decimale breuk.

Vervolgens legt een vertegenwoordiger van elke groep de oplossing uit dit voorbeeld leerlingen van een andere groep op het bord. Studenten wisselen meningen uit en trekken conclusies uit de resultaten van het oplossen van het probleem:

Het aantal decimalen in de factoren is hetzelfde aantal decimalen in hun product.

Vervolgens geeft de leerkracht commentaar op het werk van de groepen, vat de resultaten samen en trekt een conclusie.

De leerlingen schrijven in hun notitieboekje.

Conclusie: Om decimale breuken te vermenigvuldigen, moet je:

1) vermenigvuldiging uitvoeren zonder op komma's te letten;

2) Scheid in het resulterende product met een komma zoveel cijfers aan de rechterkant als er na de komma staan ​​in beide factoren samen.

3.2 Analyse van verschillende voorbeelden.

Doel: Verdere ontwikkeling van vaardigheden in het vermenigvuldigen van decimale breuken.

Laten we deze getallen vermenigvuldigen zonder op komma's te letten, en we krijgen het getal 20.496 in het product. In de twee factoren achter de komma zijn er in totaal drie decimalen. Daarom moet je in het product drie cijfers aan de rechterkant scheiden. Het product is dus gelijk aan 20,496.

VI .Problemen oplossen

Doel: Oefenen met het vermogen om de regel van het vermenigvuldigen van decimale breuken toe te passen bij het oplossen van problemen.

De leerlingen werken in tweetallen.

Taken uitvoeren: nr. 812, nr. 814

VII . De les samenvattend. Reflectie

Doel: Ga na of leerlingen de lesdoelen hebben behaald, zodat daar bij het plannen van de volgende les rekening mee gehouden kan worden.

Acties van studenten : Het samenvatten van uw kennis , beantwoord vragen.

Debriefingvragen .(Mondeling).

1. Wat hebben we vandaag in de klas geleerd?

2. Welk doel hebben we vandaag in de klas bestudeerd?

3. Laten we de regel voor het vermenigvuldigen van decimale breuken herhalen.

Aan het eind van de les geven de leerlingen reflectie:

Vond de les leuk/niet leuk

Doel van de les begrepen/niet begrepen

Wat ik heb geleerd, wat ik heb geleerd____________________________________________

Wat ik niet helemaal begreep ________________________________

Waar moet aan gewerkt worden____________________________________________

Beoordeling: De leraar moedigt de antwoorden en het werk van de leerlingen aan.

Huiswerk:№813 № 815